Regression, system identification and function approximation
A comprehensive Gaussian processes repository
A comprehensive repo on Gaussian processes code, literature, and model zoo.
References
- A comprehensive Gaussian processes repository. J. E. Johnson, Tech Rep 2019/12B, Universitat de Valencia, 2019.
ARX-RVM: Autorregressive eXogenous Relevance Vector Machine
Nonlinear system identification using Relevance Vector Machines (RVM). The ARX-RVM yields confidence intervals for the predictions and provides a better trade-off between accuracy and sparsity.
References
- Nonlinear system identification with composite relevance vector machines. Camps-Valls, G., Martínez-Ramón, M., Rojo-Álvarez, J.L., Muñoz-Marí, J. IEEE Signal Processing Letters, 14(4):279-282, 2007.
Deep Gaussian processes for biophysical parameter estimation
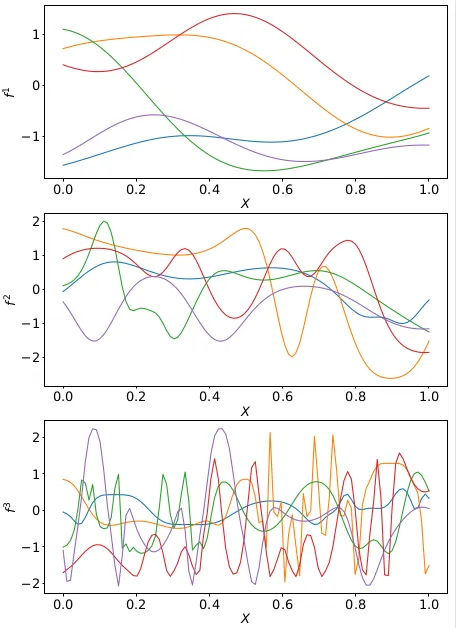
Deep Gaussian Processes (DGPs) for bio-geo-physical model inversion. Unlike shallow GP models, DGPs account for complicated hierarchical processes, provide an efficient solution that scales well to big datasets, and improve prediction accuracy over single-layer models.
References
- Deep Gaussian Processes for Parameter Retrieval and Model Inversion. Daniel H. Svendsen, Pablo M. Alvarez, Ana Belen Ruescas, Rafael Molina, and Gustau Camps-Valls, Submitted, 2020.
- Svendsen, Daniel H. et al. Deep Gaussian Processes for Geophysical Parameter Retrieval. IGARSS 2018, IEEE, 2018.
Epsilon-Huber Support Vector Regression
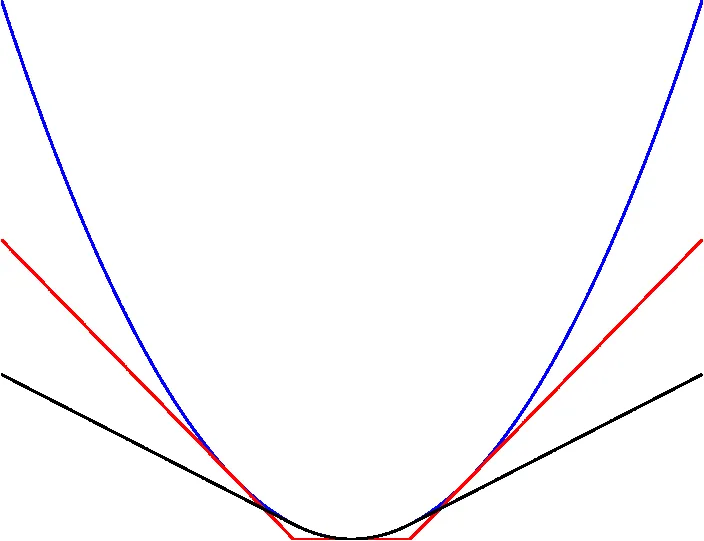
The combination of Vapnik’s e-insensitive loss function and the Huber cost function enhances performance in the presence of different noise sources. Applied to system identification, gamma-filtering, and SVR.
References
- A unified SVM framework for signal estimation. Rojo-Álvarez, J.L., Martínez-Ramón, M., Muñoz-Marí, J., Camps-Valls, G. Digital Signal Processing: A Review Journal, 26(1):1-20, 2014.
Fair Kernel Learning
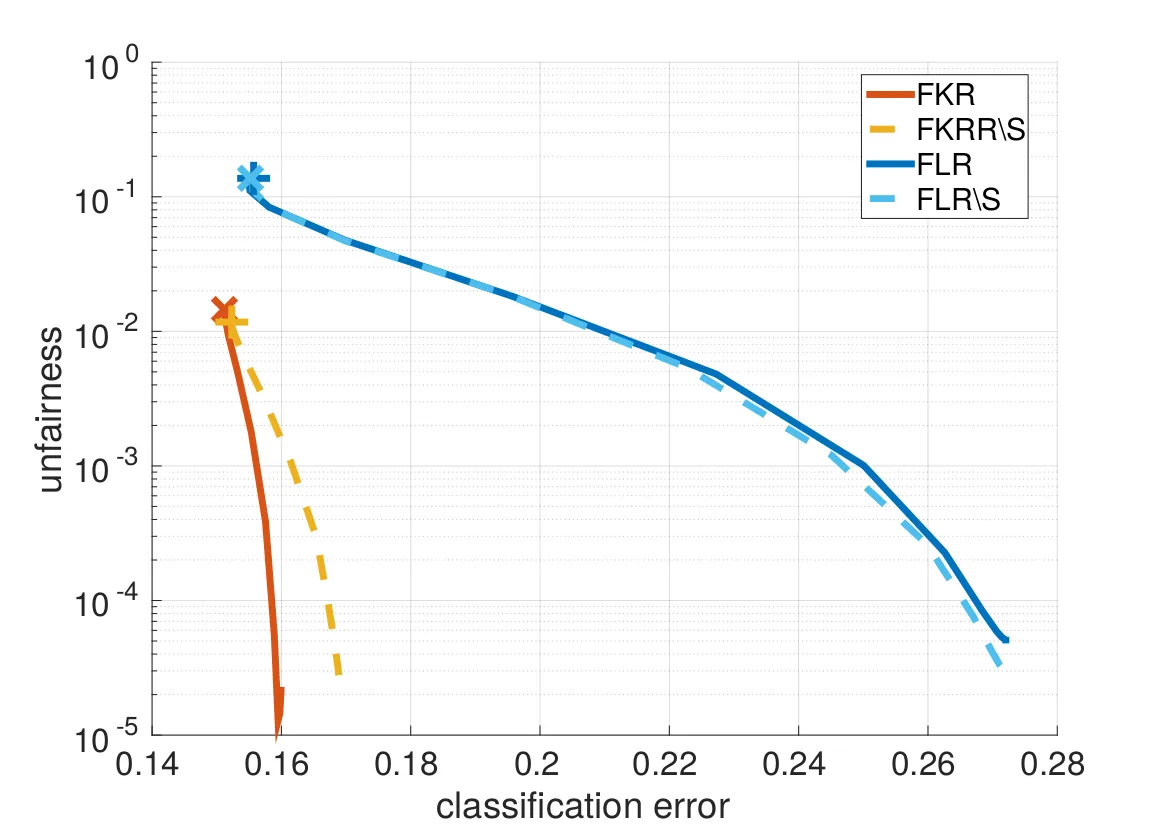
Fair Kernel Learning methods for regression and dimensionality reduction built on a previously proposed fair classification framework. The methods rely on the Hilbert-Schmidt independence criterion as the fairness term, which simplifies the problem and allows the inclusion of multiple sensitive variables simultaneously.
References
- Fair Kernel Learning. Adrián Pérez-Suay, Valero Laparra, Gonzalo Mateo-García, Jordi Muñoz-Marí, Luis Gómez-Chova, and Gustau Camps-Valls. ECML PKDD 2017 (Accepted).
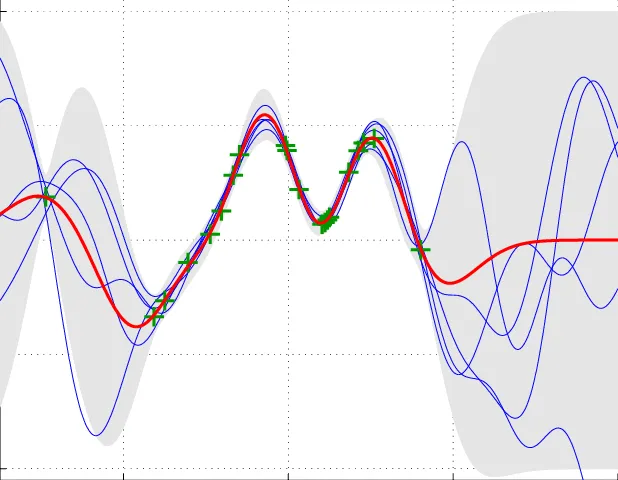
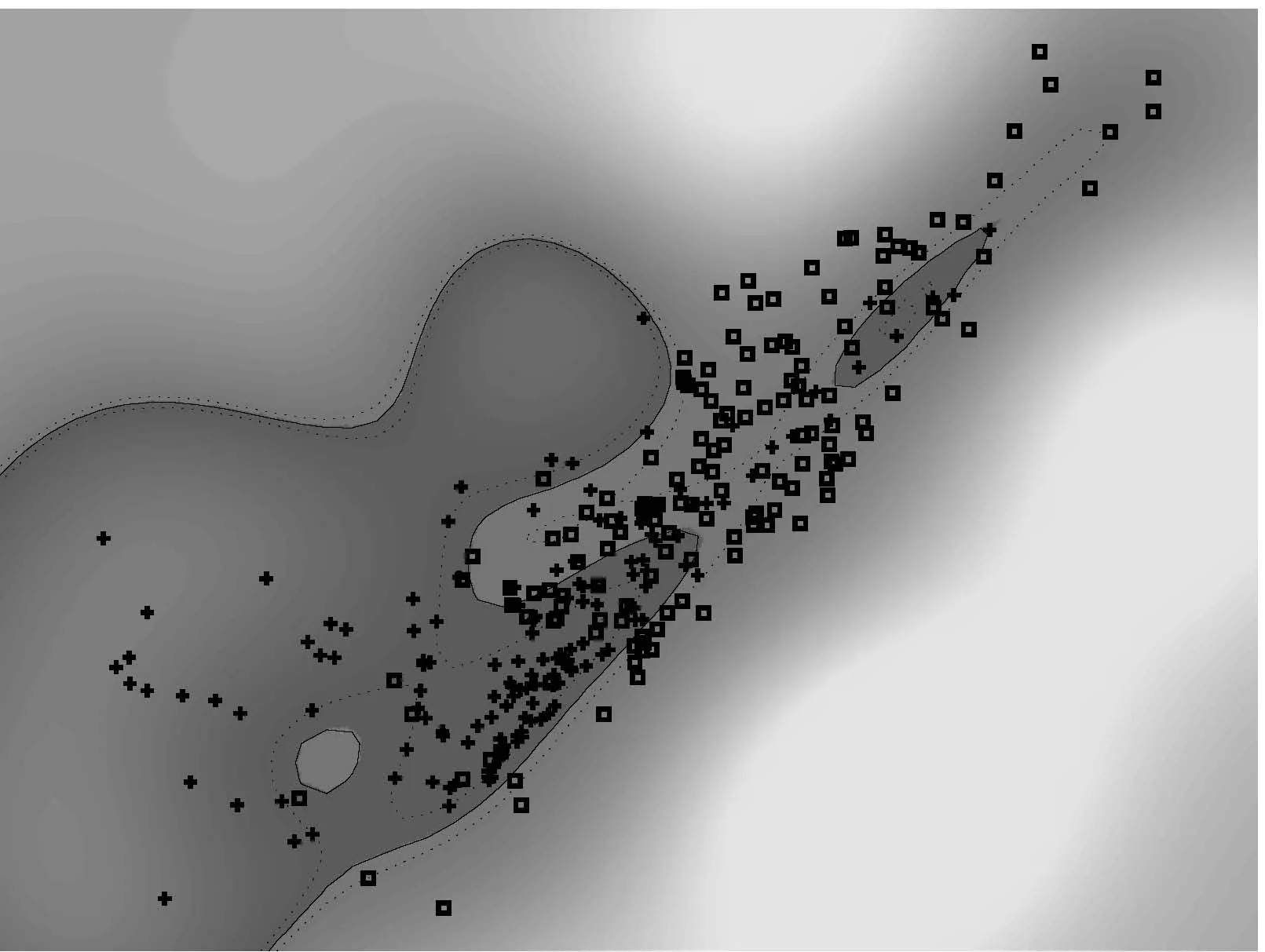
Gaussian processes with input noise
Gaussian processes with input noise.
References
- Accounting for Input Noise in Gaussian Process Parameter Retrieval. Johnson, J. E., Laparra, V., Camps-Valls, G. IEEE Geoscience and Remote Sensing Letters, 17(3):391-395, 2020.
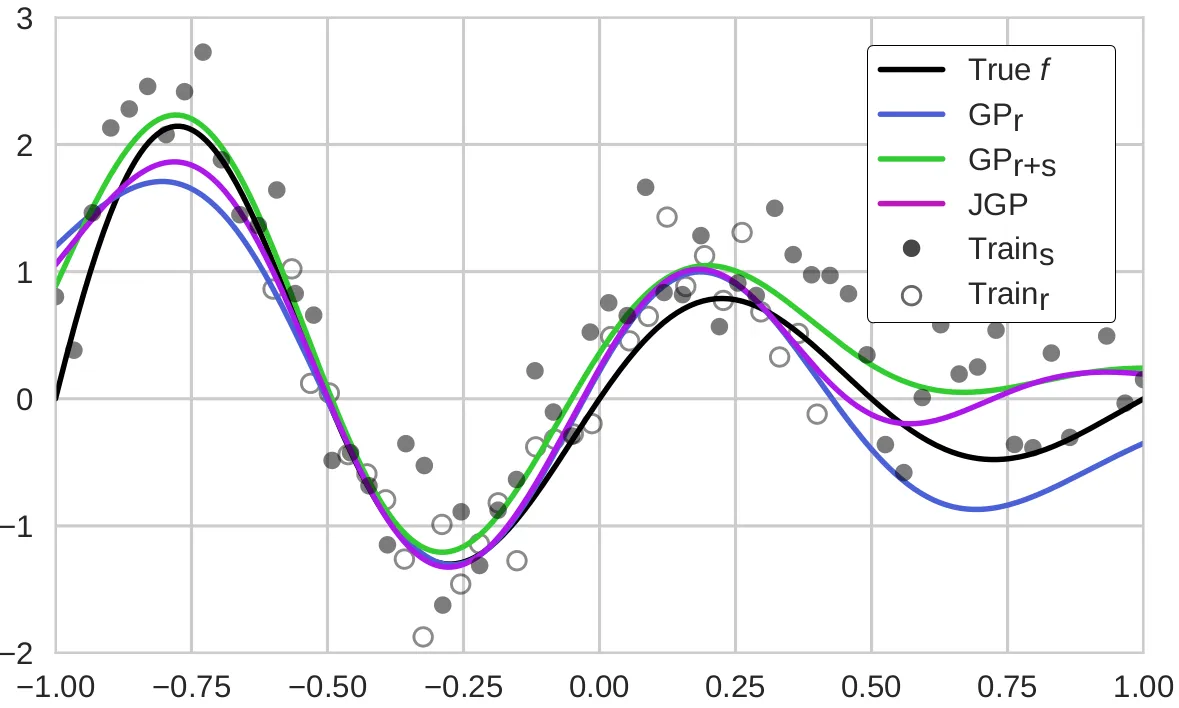
Joint Gaussian processes
A nonlinear nonparametric regression model which combines knowledge from real observations and simulated data from physical models. The Joint Gaussian Process (JGP) automatically detects the relative quality of the simulated and real data and combines them accordingly.
References
- Svendsen, D. H., Martino, L., Campos-Taberner, M., García-Haro, F. J., & Camps-Valls, G. (2017). Joint Gaussian processes for biophysical parameter retrieval. IEEE Transactions on Geoscience and Remote Sensing, 56(3):1718-1727.
- Bonilla, Edwin V., Kian M. Chai, and Christopher Williams. Multi-task Gaussian process prediction. Advances in Neural Information Processing Systems, 2008.
KARMA: Kernel AutoRegressive Moving Average with the Support Vector Machine
Nonlinear system identification using the Kernel ARMA model with Support Vector Machines (SVM). Explicitly considers an ARMA model in RKHS, resulting in improved accuracy in system identification tasks.
References
- Support vector machines for nonlinear Kernel ARMA system identification. Martínez-Ramón, M., Rojo-Álvarez, J.L., Camps-Valls, G., Muñoz-Marí, J. IEEE Transactions on Neural Networks, 17(6):1617-1622, 2006.
KSNR: Kernel Signal to Noise Ratio
The Kernel Signal to Noise Ratio (KSNR) model maximizes signal variance while minimizing noise variance in RKHS. It is especially useful for handling correlated and non-Gaussian noise.
References
- Learning with the kernel signal to noise ratio. Gomez-Chova, L., Camps-Valls, G. IEEE International Workshop on Machine Learning for Signal Processing, MLSP, 2012.
MSVR: Multioutput Support Vector Regression
M-SVR extends the single-output SVR by considering nonlinear relations between features and among the output variables, which are typically inter-dependent.
References
- Multioutput support vector regression for remote sensing biophysical parameter estimation. Tuia, D., Verrelst, J., Alonso, L., Perez-Cruz, F., and Camps-Valls, G. IEEE Geoscience and Remote Sensing Letters, 8(4):804-808, 2011.
simpleR v2.1: simple Regression toolbox
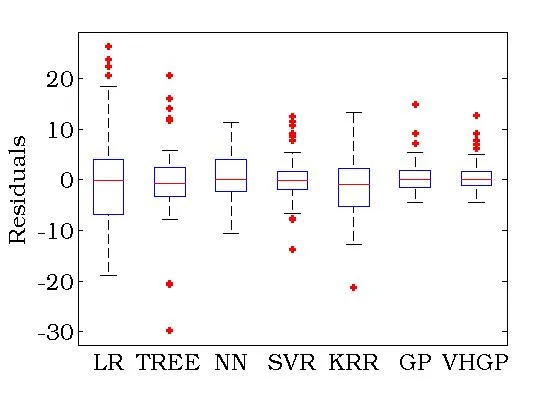
The simple Regression toolbox, simpleR, contains a set of functions in Matlab to illustrate the capabilities of several statistical regression algorithms. simpleR contains simple educational code for linear regression (LR), decision trees (TREE), neural networks (NN), support vector regression (SVR), kernel ridge regression (KRR), Gaussian Process Regression (GPR), and Variational Heteroscedastic Gaussian Process Regression (VHGPR). A dataset of spectra and associated chlorophyll content is included to illustrate training/testing procedures.
References
- Retrieval of biophysical parameters with heteroscedastic Gaussian processes. Lázaro-Gredilla, M., Titsias, M.K., Verrelst, J., and Camps-Valls, G. IEEE Geoscience and Remote Sensing Letters, 11(4):838-842, 2014.
- Prediction of daily global solar irradiation using temporal Gaussian processes. Salcedo-Sanz, S., Casanova-Mateo, C., Muñoz-Marí, J., and Camps-Valls, G. IEEE Geoscience and Remote Sensing Letters, 11(11):1936-1940, 2014.
SS-SVR: Semi-supervised Support Vector Regression
Semi-supervised SVR algorithms tested in multiplatform LAI estimation and oceanic chlorophyll concentration prediction, showing good generalization capabilities when few labeled samples are available.
References
- Biophysical parameter estimation with a semisupervised support vector machine. Camps-Valls, G., Munoz-Marí, J., Gómez-Chova, L., Richter, K., and Calpe-Maravilla, J. IEEE Geoscience and Remote Sensing Letters, 6(2):248-252, 2009.